一篇小论文
我们学校要求一学年要写出一篇小论文,这是我今年和@railgunjjj 写的
大家看看也就图个乐呵,没什么专业性
摘要
本篇文章主要使用Logistic 生长曲线预测上海3~5月份的疫情数据,以及浅显的介绍传统传染病模型“SEIR”,并分析中国的抗疫策略
引言
由于近期(2022年12月4日)的上海疫情的发展形式较稳定,所以本篇文章专门研究于(2022年3月~2022年5月)的疫情数据预测
预测新冠的走势有很多种方法,比如通过构建统计学模型、数学模型,或者利用机器学习、深度学习方法拟合疫情发展趋势,利用历史数据对未来的确诊病例等疫情形势进行预测,比如说,逻辑斯蒂生长曲线拟合数据,预测未来几天可能的发展趋势;或者利用时间序列模型构建预测模型;也可用LSTM构建预测模型,一种特殊的RNN网络。以上方法,除生长曲线外,其他模型,需要大量数据做训练,就目前情况看,数据量并不大,即使构建出模型,参考价值并不大,并没有与业务做融合,只是以数据理解数据。
另外一个建模思路,可以从传统疾病传播模型(SIS、SIR、SEIR等),建立传染病模型,结合此次冠状病毒的传播特性,建立适当的传染病数学模型,就能够较为精准的预估疫情的发展趋势。
因本人不具备传染病、医疗专业领域相关知识,从非专业角度,尝试利用Logistic生长曲线模拟上海地区累计确诊病例数量,并试着简单叙述传统疾病传播模型-SEIR
模型介绍
(一)Logistic生长曲线
逻辑斯蒂曲线是由比利时数据学家首次发现的特殊曲线,后来,生物学家皮尔(R.Pearl)和L·J·Reed根据这一理论研究人口增长规则,因此,逻辑斯蒂生长曲线也被称为生长曲线或者珍珠德曲线。逻辑斯蒂生长曲线一般形式如下:
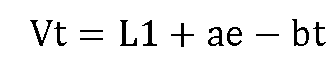
(二)SEIR传统传染病模型
 常见的传染病模型按照具体的传染病的特点可分为 SI、SIS、SIR、SIRS、SEIR 模型。其中“S”“E”“I”“R”的现实含义如下:(如上图所示)
常见的传染病模型按照具体的传染病的特点可分为 SI、SIS、SIR、SIRS、SEIR 模型。其中“S”“E”“I”“R”的现实含义如下:(如上图所示)
S (Susceptible),易感者,指缺乏免疫能力健康人,与感染者接触后容易受到感染;
E (Exposed),暴露者 ,指接触过感染者但不存在传染性的人,可用于存在潜伏期的传染病;
I (Infectious),患病者,指有传染性的病人,可以传播给
S,将其变为 E 或 I ;
R (Recovered),康复者,指病愈后具有免疫力的人,如是终身免疫性传染病,则不可被重新变为 S 、E 或 I ,如果免疫期有限,就可以重新变为 S 类,进而被感染。此模型无解析解,给定 λ、δ、μ、s0、i0 可求数值解。
代码实现
(一)Logistic生长曲线
import pandas as pd csv_file = "covid19_3.csv" df = pd.read_csv(csv_file, encoding="utf-8") from scipy.optimize import curve_fit import urllib import json import numpy as np import matplotlib.pyplot as plt import pandas as pd import time csv_file = "covid19_3.csv" def logistic_function(t, K, P0, r): t0 = 0 exp = np.exp(r * (t - t0)) return (K * exp * P0) / (K + (exp - 1) * P0) def predict(province_code): predict_days = 10 # 预测未来天数 df = pd.read_csv(csv_file, encoding="utf-8") df = df[df.province_code == province_code] confirm = df['confirmed'].values x = np.arange(len(confirm)) # 用最小二乘法估计拟合 popt, pcov = curve_fit(logistic_function, x, confirm) print(popt) # 近期情况预测 predict_x = list(x) + [x[-1] + i for i in range(1, 1 + predict_days)] predict_x = np.array(predict_x) predict_y = logistic_function(predict_x, popt[0], popt[1], popt[2]) print(predict_y) ########################################################################################################################## # 绘图 plt.figure(figsize=(15, 8)) plt.plot(x, confirm, 's', label="confimed infected number") plt.plot(predict_x, predict_y, 's', label="predicted infected number") # plt.xticks(predict_x, date_labels[:len(predict_x) + 1], rotation=90) plt.yticks(rotation=90) plt.suptitle( "新冠感染人数的 Logistic 拟合曲线 (Max = {}, r={:.3})".format(int(popt[0]), popt[2]), fontsize=16, fontweight="bold") plt.title("Predict time:{}".format(time.strftime("%Y-%m-%d", time.localtime())), fontsize=16) plt.xlabel('date', fontsize=14) plt.ylabel('infected number', fontsize=14) plt.plot() plt.show() province_codes = [1] for province_code in province_codes: predict(province_code)
(二)SEIR传统传染病模型
import numpy as np import matplotlib import matplotlib.pyplot as plt import pandas as pd import pylab # 计算SEIR的值 def calc(T): for i in range(0, len(T) - 1): S.append(S[i] - r * beta * S[i] * I[i] / N - r2 * beta2 * S[i] * E[i] / N) E.append(E[i] + r * beta * S[i] * I[i] / N + r2 * beta2 * S[i] * E[i] / N - alpha * E[i]) I.append(I[i] + alpha * E[i] - gamma * I[i]) # 计算累计确诊人数 R.append(R[i] + gamma * I[i]) # 画图 def plot(T, S, E, I, R): plt.figure() plt.title("SEIR-Time Curve of Virus Transmission") plt.plot(T, S, color='r', label='Susceptible') plt.plot(T, E, color='k', label='Exposed') plt.plot(T, I, color='b', label='Infected') plt.plot(T, R, color='g', label='Recovered') plt.grid(False) plt.legend() plt.xlabel("Time(day)") plt.ylabel("Population") plt.show() S, E, I, R = [], [], [], [] N = 10000 # 人口总数 I.append(1) S.append(N - I[0]) E.append(0) R.append(0) r = 20 # 传染者接触人数 r2 = 30 beta = 0.03 # 传染者传染概率 beta2 = 0.03 # 易感染者被潜伏者感染的概率 alpha = 0.14 # 潜伏者患病概率 1/7 gamma = 0.1 # 康复概率 pylab.rcParams['figure.figsize'] = (12.0, 7.0) T = [i for i in range(0, 100)] calc(T) plot(T, S, E, I, R)
(三)部分数据

代码结果
(一)Logistic 拟合曲线
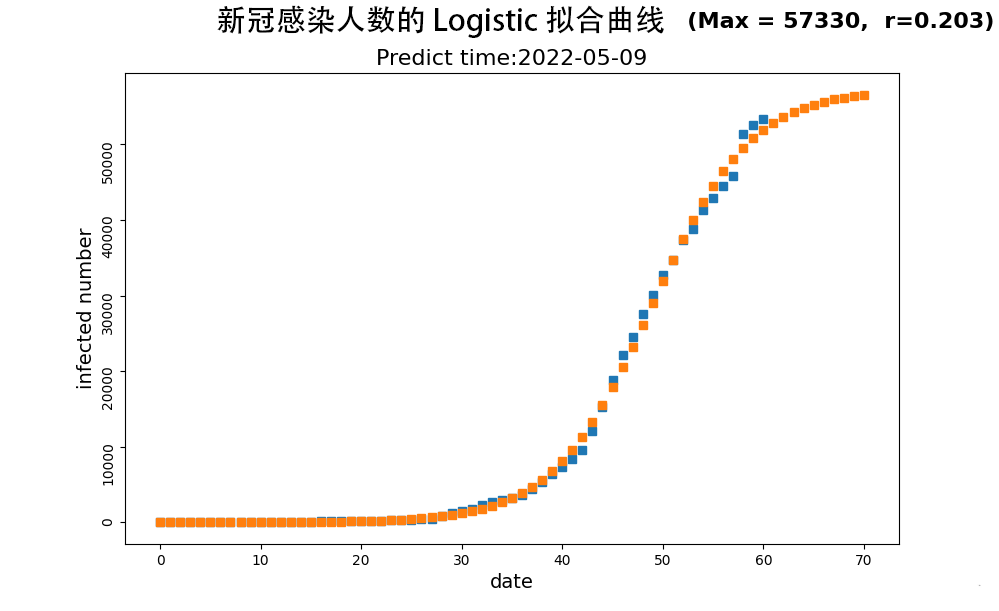
截止于5月9号,新冠确诊的实际人数是55599、55921、56155(分别为5月7日、5月8日、5月9日的数据),如上图所示,根据此模型预测这三天的确诊人数分别为55926、56179、56387,可见预测值与实际值基本一致。
(二)SEIR传统传染病模型
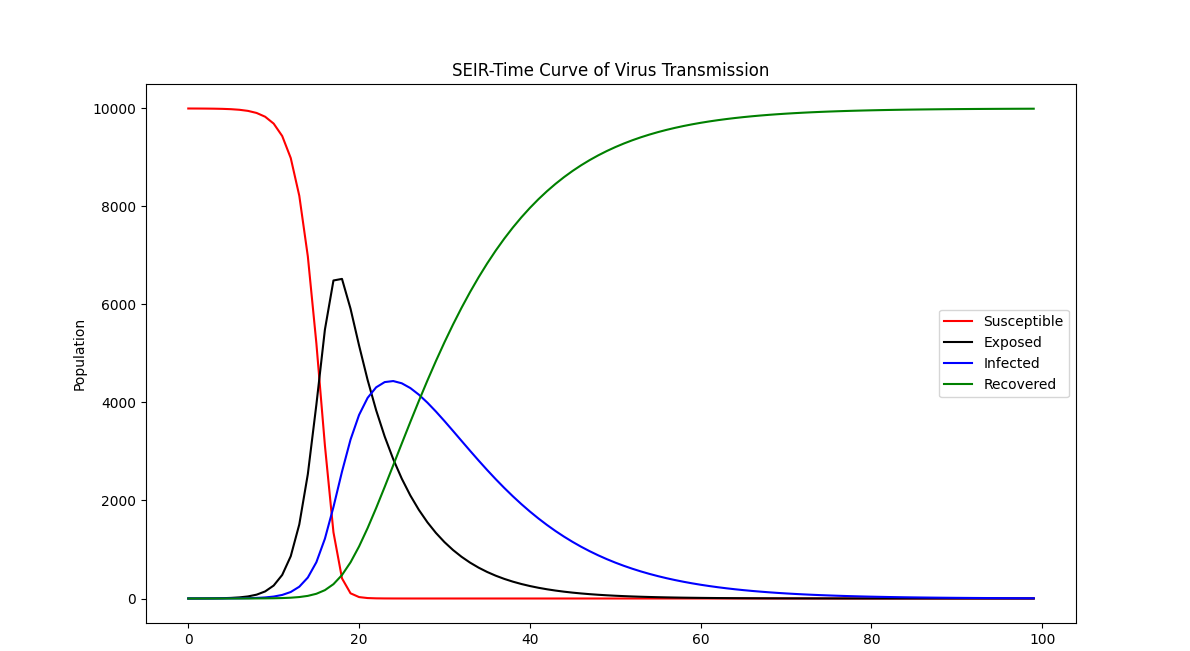
我们这里不在运用采集到的数据来模拟疫情的发展形式,一方面原因是我们并不能较好的估计模型中涉及到各个参数, 需要考虑的的参数较多,另一方面数据并不能支撑其模型推导,特别是疫情的干预因素、社会舆情因素,对疫情发展趋势都会产生一定的影响,应将相关的因素考虑进去,所以这个问题相对来说是比较复杂的过程,我们这里不再进行过多探讨。
中国的抗疫策略分析
(一)近期疫情情况综述(以上海为例)
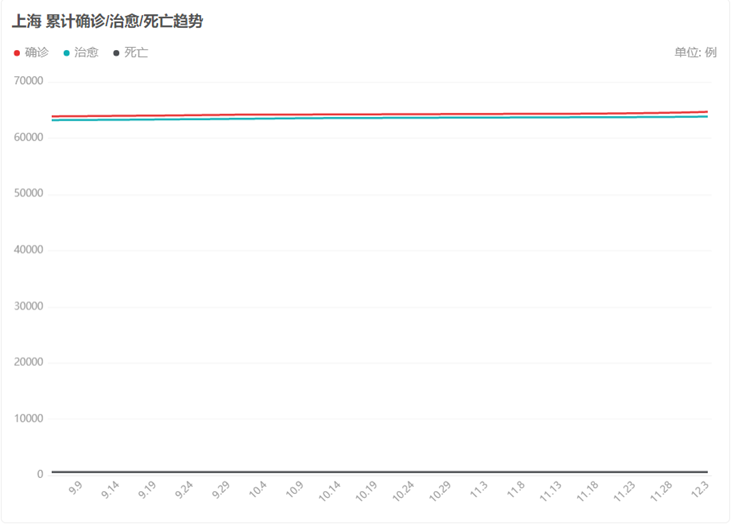
上图为上海累计确诊/治愈/死亡趋势(截至2022/12/3)。
摘自
https://voice.baidu.com/act/newpneumonia/
,从图中大致可以看出在图中的3月内,死亡人数、确诊人数暂未出现明显的波动,与2020年初疫情形势有较大不同,这说明了上海在新型冠状病毒上的医疗技术已经得到改进,疫情形势没有像2020年初那么严峻,策略也需要得到改变。(二)防疫新政策解读(以上海为例)
近日,上海于11月13日下午正式发布“优化防控7条措施”。
一是对密切接触者,管理措施由“7天集中隔离+3天居家健康监测”调整为“5天集中隔离+3天居家隔离”。
二是及时准确判定密切接触者,不再判定密接的密接。
三是将风险区由“高、中、低”三类调整为“高、低”两类,高风险区连续5天未发现新增感染者,降为低风险区。
四是对入境人员,管理措施由“7天集中隔离+3天居家健康监测”调整为“5天集中隔离+3天居家隔离”。
五是明确入境人员阳性判定标准为核酸检测Ct值<35。
六是优化校园核酸检测频次,中小学(含中职校)和托幼机构每周一、三、五进行校内核酸检测,核酸检测相关要求根据疫情形势进行动态优化调整。
七是一般不再按行政区域开展全员核酸检测,只在感染来源和传播链条不清、社区传播时间较长等疫情底数不清时开展。同时,进一步组织好常态化核酸检测和社区便民筛查。
从以上措施中,我们可以发现上海市主要在密切接触者上、入境人员上、区域划分上、教育上对于防疫政策进行了一定程度上的可行性调整,严格执行了国务院联防联控机制发布的《关于进一步优化新冠肺炎疫情防控措施科学精准做好防控工作的通知》,加大了上海市“科学精准防疫”的力度,采取了比之前的政策更果断、有效的措施,最大限度减少疫情对市民正常工作的影响。
(三)对于未来防疫政策的新设想(以上海为例)
11月13日上海市发布的新政策体现出“科学精准防疫”的政策是未来政策的主要趋势,对于这种趋势,我提出以下建议。
- 继续推动“全民疫苗”,让市民拥有较强的免疫能力,同时对核酸码、随申码等进行改进(如推出老年机专用核酸码等)
- 在核酸时采用一楼一管等政策,方便居民委员会定位,更“精准”,更“有效”。
- 在更多学校的小区内添加防疫智能设备,方便学校统计。
参考文献
[1]马思婕,黄珈铭,印英东,曾楚仪.基于SEIR模型的COVID-19传染力研究[J].江苏科技信息,2022,39(10):73-76.
[2]徐方,陆殷昊,黄晓燕.logistic模型在新型冠状病毒肺炎疫情中的应用[J].实用预防医学,2022,29(06):762-766.
[3]叶红霞,刘应辉,吴凌逸.基于SEIR模型对接种新冠病毒疫苗的预测与控制[J].哈尔滨师范大学自然科学学报,2022,38(02):30-36.
[4]王博云,刘天禹,李露凝,李强,贾鹏飞,陈晋.中国COVID-19疫情扩散的时空模式及影响因素[J].地理学报,2022,77(02):443-456.
[5]余小军,王昌晶,屈文建,左正康,罗海梅.COVID-19疫情传播建模分析[J].江西师范大学学报(自然科学版),2021,45(06):559-565.DOI:10.16357/j.cnki.issn1000-5862.2021.06.02.
[6]冯苗胜,王连生,林文水.Logistic与SEIR结合模型预测新型冠状病毒肺炎传播规律[J].厦门大学学报(自然科学版),2020,59(06):1041-1046.
[7]学会微笑.上海进一步优化疫情防控措施(7条)[N].上海本地宝.2022.11.16






好家伙
未来可期
好家伙,什么学校,厉害厉害
666
太强了,这就是大城市的学校吗,未来可期啊
复旦大学第二附属学校-初中

666666666666666666666666666666666666666666