还不知道递归是什么?
递归是什么?
一个函数自己代入自己,就可以叫做递归
先来看看一个公式,这个公式是求一个实数的乘阶
公式的意思是当n值为0的时候则函数返回为1, 其他实数则执行递归步骤
给这个公式带入实数4
可以看到这个就是数学上的递归,当这个函数被应用的时候,这个公式就会一直递下去直到满足初始值的条件后则开始归,然后开始计算从后往前一直计算值

可以直接带入到计算机中,也是同理
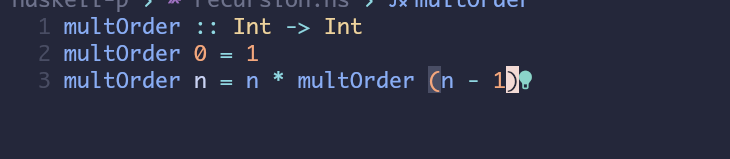
这是haskell中的一个函数,很符合上面乘阶公式的定义,当传入的值是0的时候返回1,其他时候就是递归调用自身
再来看看python跟js的

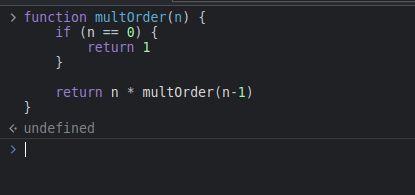
这几个语言都是等价的

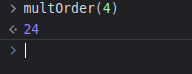
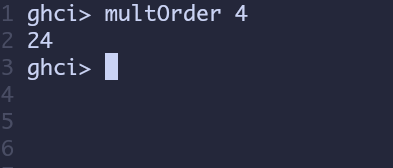
递归的时候一般把if n == 0 -> //dosomething的这个条件当作递归的出口,如果一个递归没有递归出口,那么这个递归将永远的递下去,无法结束,在程序中就会看到一个经典的错误stack overflow, 为什么会出现这个错误呢?
可以看到上面的数学公式,当每次计算过程中都会保留之前的数,也就是
每次调用自身的时候,都会有一个表达式保留在了栈里 4 x (3 x (2 x (1 x ...))),这个表达式的层数会随着递归的次数越多而越大,直到把整个栈的空间给挤满然后溢出,就发生了错误
一般把保留在栈里的这个操作叫保存现场
所以递归不能太深
那么有没有不保存现场的递归呢?有的,这个叫尾递归
还是那个乘阶, 不过得加上一个辅助函数,这个辅助函数的公式如下
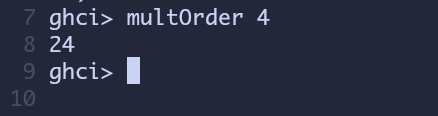
给公式带入4
尾递归的原理是什么呢?就是把本来要保留等带条件结束返回的表达式,直接求值并且通过参数来传递下去,这样栈就减少了保存现场的开销,只有压栈出栈以及保留栈帧的开销了,没有额外的使用太多的空间,所以就会性能就会大大的提升,也会减少空间的使用,增加递归的深度
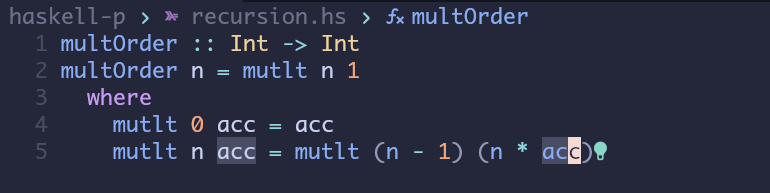
这是haskell的实现
这是python跟js的实现


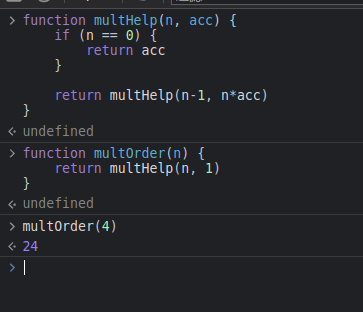
但是尾递归并不是没有任何的额外空间开销的,在调用的时候还是每次调用还是会保留传入的参数,也就是说,帮助函数的栈里还保留有每次传参的参数。
比如说第一次调用(4, 1)栈里保留就会保存有[4,1],第二次调用就是[4, 1, 3, 4, 2, 12]第三次调用就是等等,这样依次下去。
这个时候就出现了一个技术是叫做尾递归优化,如果你的递归是尾递归的话,编译器就会对你的代码进行优化,有的编译器会直接把你这里的代码优化成一个循环,但是更多的是优化栈,每次你传参从[4, 1, 3, 4, 2, 12]这样增长的栈给优化成每次计算都出栈入栈保持栈是空的状态,例如第一次调用栈是这样的[4,1], 第二次调用栈是这样的[3, 4],第三次[2, 12],这样就没有额外的内存开销了,这个时候的尾递归,基本等价于循环




知识增加*1
再写的简单点 少点数学知识
讲讲递归在项目中的使用 ,和循环有什么区别,可以再将深入一点,比如尾递归什么的,这样就能充实我的知识辣😋
真的是,学到老活到老!