Haskell 随笔二 λ演算

前言

image.png

应猫猫的要求，这次就说一下λ演算吧

本文记录一下个人学习Haskell的一些随笔，记录一下学习Haskell过程中的一些有趣的东西

Haskell语言的思维可能颠覆绝大多数鱼友对编程语言的认知

因为是随笔，可能继续更新也可能不继续更新

上一期帖子 Haskell 随笔一 函数式编程

随笔二 λ演算 （lambda calculus）

λ演算是一个计算机科学理论，甚至比图灵机都早，在上个世纪30年代往前，并没有通用计算机，都是针对特定的领域定制的计算机。λ演算更贴合软件的计算方式，并没有像图灵机那样贴合硬件。正因为这个原因所以现有计算机都是按照图灵机的计算模型进行设计的。

在说λ演算之前先说一个重要的概念，那就是前缀表达式

前缀表达式

前缀表达式跟我们人类书写的1 + 1中缀表达式不太一样，前缀表达式是符号在前面+ 1 1

前缀表达式其实比中缀表达式更适合计算机进行计算，在规则的抽象下，中缀表达式的优先级规则比如()[]等比前缀表达式更加复杂，比如这个表达式(1+1)* 5因为要保证1+1要优先于*5所以得给1+1加上一个()来进行优先级升级，计算机需要先找到优先级最高的再进行解析算法复杂度比较高。

前缀表达式只需要按顺序结合就可以进行计算，比如像刚才的算式(1+1)*5转换成前缀表达式就是这样的 * + 1 1 5只需要读取表达式，一个表达式读取完成就可以进行计算。

方便理解我贴出函数来应用的方式Mul(Add(1, 1), 5)，可以看到函数的调用其实是和前缀表达式是一样的，是一个左结合的方式进行计算，从左往右依次读取读到最后，然后再进行计算，λ演算也是如此，请记住这一个概念

λ表达式（项）

由以下规则来构成一个λ表达式

  • 变量 变量是数学意义上的变量，只能绑定不能进行修改，和c语言的宏中的#define相似
  • 抽象 是一个完整的函数定义，λx.M,这里的x是一个变量(可以直接理解为参数)，M是一个完整的λ表达式，M表达式中的x都会绑定成变量x
  • 应用 (M N)将M函数作用于参数N, MN均是λ表达式

知道规则后让我们来定义一个λ表达式来方便理解吧

\begin{aligned} &(\lambda x\;y.x + y)\;1\;2\\ &=1 + 2\\ &=3 \end{aligned}

这是一个完整的λ表达式，λ用于表明这是一个λ表达式，后面跟着的xy则是参数，x+y则是函数体，函数体中的xy变量与参数绑定，然后一个括号把表达式包裹起来，表示整个λ表达式的定义已经结束了，这是在消除λ表达式的歧义，相当于把表达式存入到了括号里，紧接着的1和2则是应用，然后计算得出3。

\begin{aligned} &plus = λx\;y.x+y\\ &plus\;1\;2 =3 \end{aligned}

这是没有括号的版本，这样把λ表达式绑定给了plus这个变量，然后再进行应用，这样分成了两个表达式，这样就不需要用括号消除函数和应用的表达式在一起的歧义了

可以看出这里的λ表达式和前缀表达式里的+号是做同样的事情，把(\lambda x\;y.x + y)替换成+号就变成了+ 1 2，与前缀表达式一样，λ表达式的应用都是左结合的，从左往右计算，先把1进行应用\lambda x\;y.1+y，然后再和2应用，就是\lambda x\;y.1+2，这样就得到了3，整个过程是这样的((plus\;1)\;2)=3

是不是和主流语言里的匿名函数很像？

python (lambda x,y: x + y)(1, 2)

js ((x, y) => x + y)(1, 2)

rust (|x, y| x + y)(1, 2)

golang (function (int x,y) int { return x + y })(1, 2)

php (fn($x, $y) => $x + $y)(1, 2)

Haskell (\x y -> x + y) 1 2

chez scheme ((lambda (x y) (+ x y)) 1 2)

这些都是做λ表达式在各个语言中的应用。

λ演算里只有一个类型，那就是λ表达式，一切都是由λ表达式来抽象的。

再值得一提的是上面这几个语言中除了Haskell是像我说的((plus\;1)\;2)这样的逐步应用，其他的都是直接把1和2一起应用的，就像这样plus(1,2)。

为什么Haskell是逐步应用的就涉及到了它本身的特性就不在本文展开，挖个坑以后有机会再说trollface

不过Haskell也是可以做到一起应用的操作就像这样(\(x, y) -> x + y)(1,2)，把参数设置成一个元组，就可以做到同时应用了，是不是很棒～

接下来后续的代码我都将用Haskell来进行演示

规约

λ演算是创建λ表达式，以及规约对λ表达式进行优化的操作，上面说完了创建，现在来说说规约。

α转换（alpha conversion）

α转换是对λ表达式中的变量进行重命名的操作

比如这里有一个λ表达式

\x y -> x + y

使用ɑ转换后

\a b -> a + b

这样虽然名字变量的名字不相同，但是这两个函数是等价的，使用后将会得到同样的效果

在演算中允许在同一个作用域内对一个λ表达式进行ɑ转换，但是也没那么简单，如果把\x -> x + y中的x转换成y之后，函数就变成了\y -> y + y这样的结果，这样函数的函数明显的和转换前并不等价。

β化简 (Beta reduction)

β化简是对λ表达式的一个化简的操作，将表达式替换成带入后的表达式进行最大化简

比如这里有一个λ表达式应用

(\x -> 2*x*x + y) 7

使用β化简后，整个表达式就会被替换成这样

2*7*7 +y

然后再进行化简

98 + y

看下去就知道这里的化简其实并不是单纯的求值

η转换 (Eta conversion)

η转换是会将表达式转换成另一个等价的更简约的表达式

比如这里有一个λ表达式

\x -> abs x

使用η转换后就会被替换成

abs

因为这个表达式的本身就是在做abs的求值，但是在求值的层面上再添加了一个抽象，多了一次函数调用的开销，所以使用η转换将表达替换成等价但更简约快速的表达式

再比如\x -> x + 1这个表达式将会被转换成(+1)这样的表达式

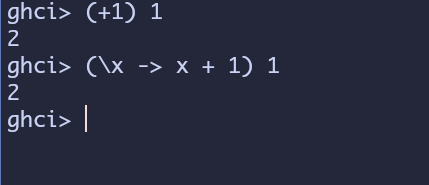
image.png

λ演算构建的计算机体系

说了那么多，你们可能会想，怎么用λ演算来构建最基础的体系呢？是怎么做到只用λ表达式来抽象万物的呢？

邱奇编码，是的就是那个提出λ演算的人，现在就用邱奇编码来抽象一些图灵机的东西吧，但是抽象前先记住λ演算中的所有算式都适用于规约进行优化

抽象Bool和IF

先让我们来构建一下一个最简单的bool代数吧

bool代数只有两个值，那就是true和false

true = \f x -> f

false = \f x -> x

既然有了真和假，那我们来构建代码中最主要的一个逻辑控制，那就是if,因为if在Haskell中是关键词，所以这里用iF来做代替

iF = \b t f -> b t f

这样if就抽象好了

来实际的应用一下一个最常见的条件分支

if bool then
    code1
else
    code2

image.png

是不是很神奇？抽象出了条件分支，防止有些鱼油没看明白这里将用公式来解释一下

iF true 1 2的时候是在做了这个运算

\begin{aligned} &(\lambda b\; t\; f.b\;t\;f)(\lambda f\;x.f)\;1\;2\\ &=(\lambda f\;x.f)\;1\;2\\ &=1 \end{aligned}

iF false 1 2的时候是在做这个运算

\begin{aligned} &(\lambda b\; t\; f.b\;t\;f)(\lambda f\;x.x)\;1\;2\\ &=(\lambda f\;x.x)\;1\;2\\ &=2 \end{aligned}

抽象逻辑运算符

ok,既然都抽象了bool和if来，那当然少不了or and 还有not了呀

or = \x y -> iF x true y

and = \x y-> iF x y false

not = \x -> iF x false true

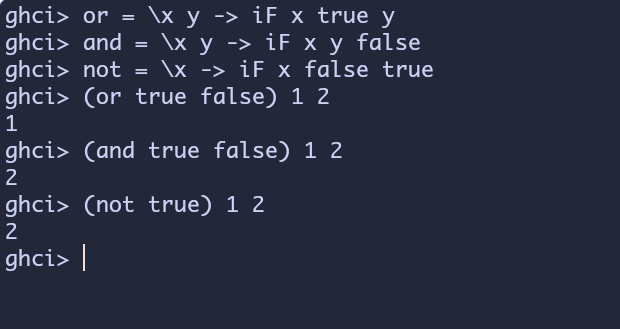
image.png

用公式来解释是这样的

\begin{aligned} ((or\;true\;false)\;1\;2)&=(\lambda x\;y.IF\;x\;true\;y)(true)(false)\;1\; 2\\ &=((\lambda b\;t\;f.b\;t\;f)(\lambda f\;x.f)(\lambda f\;x.f)(\lambda f\;x.x))\;1\; 2\;\\ &=(\lambda f\;x.f)(\lambda f\;x.f)(\lambda f\;x.x)\;1\;2\\ &=(\lambda f\;x.f)\;1\;2\\ &=1 \end{aligned}
\begin{aligned} ((and\;true\;false)\;1\;2)&=(\lambda x\;y.IF\;x\;y\;false)(true)(false)\;1\; 2\\ &=((\lambda b\;t\;f.b\;t\;f)(\lambda f\;x.f)(\lambda f\;x.f)(\lambda f\;x.x))\;1\; 2\;\\ &=(\lambda f\;x.x)(\lambda f\;x.f)(\lambda f\;x.x)\;1\;2\\ &=(\lambda f\;.x.x) \;1\;2\\ &=2 \end{aligned}
\begin{aligned} (not\;true)\;1\;2)&=(\lambda x.IF\;x\;false\;true)(true) \;1\; 2\\ &=((\lambda b\;t\;f.b\;t\;f)(\lambda f\;x.f)(\lambda f\;x.x)(\lambda f\;x.f))\;1\; 2\;\\ &=(\lambda f\;x.f)(\lambda f\;x.x)(\lambda f\;x.f)\;1\;2\\ &=(\lambda f\;.x.x) \;1\;2\\ &=1 \end{aligned}

换成鱼油最常见的写法就是这样

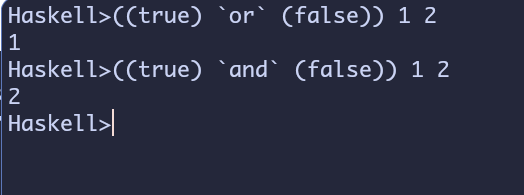
image.png

抽象正整数

记得前面说过的一句话吗？λ演算里只有一个类型，那就是λ表达式，一切都是由λ表达式来抽象。是的这里说的一切也包括数字，在λ演算中，连数字也是用λ表达式来抽象的，并不像图灵机那样用二进制来抽象。接下来开始演示一下一部分的抽象来验证λ演算是图灵完备的

由于常数在Haskell中是字面量，所以这里就用英文来代替阿拉伯数字

zero  = \f x -> x
one = \f x -> f x
two = \f x -> f (f x)
tree = \f x -> f (f (f x))
four = \f x -> f (f (f (f x)))
....

常数是没边界的我这里只用这几个来做演示

这些就是在λ演算中的常数了，邱奇编码的表示方式，这些常数就是用这些λ表达式来表达的。

0就是\lambda f\;x.x

1就是\lambda f\;x.f\;x

但是这样看的话会很累，所以为了方便理解，我写一个能把邱奇编码转换成指定的整数的函数方便查看

toInt = \f -> f (+1) 0

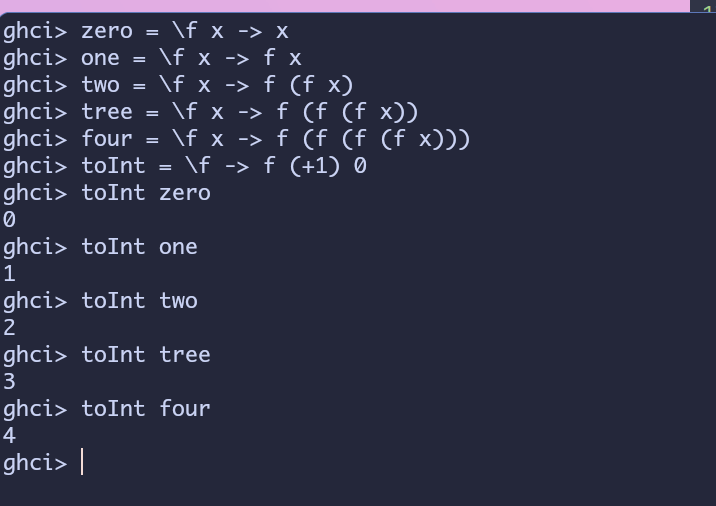
image.png

\begin{aligned} (toInt\;zero) &= (\lambda f.(f\;(\lambda x.x+1))\;0)(\lambda f\;x.x)\\ &=(\lambda f.(\lambda f\;x.x)(\lambda x.x+1)\;0)\\ &=0\\ \end{aligned}

很好，现在能让抽象可以可视化之后，再来实现一些常数的运算

抽象后继运算（i++）

succ = \n f x -> f (n f x)

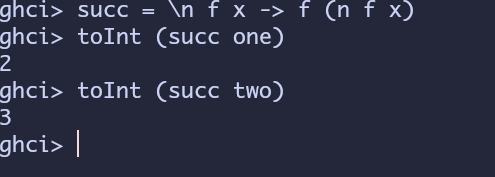
image.png

image.png

公式

\begin{aligned} (succ\;one) &= (\lambda n\;f\;x.f\;(n\;f\;x))(\lambda f\;x.f\;x)\\ &=(\lambda f\;x.f\;((\lambda f\;x.f\;x)\;f\;x))\\ &=(\lambda f\;x.f\;(f\;x))\\ &=2\\ (succ\;two) &= (\lambda n\;f\;x.f\;(n\;f\;x))(\lambda f\;x.f\;(f\;x))\\ &= (\lambda f\;x.f\;(\lambda f\;x.f\;(f\;x)\;f\;x))\\ &=(\lambda f\;x.f\;(f\;(f\;x)))\\ &=3 \end{aligned}

抽象加法

plus = \n m f x -> n f (m f x)

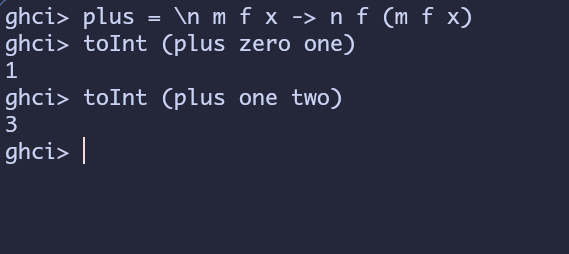
image.png

用公式来解答

\begin{aligned} (plus\;zero\;one) &= (\lambda n\;m\;f\;x.n\;f\;(m\;f\;x))(\lambda f\;x.x)(\lambda f\;x.f\;x)\\ &=(((\lambda f\;x.x)\;f) (\lambda f\;x.f\;x))\;f\;x\\ &=(\lambda f\;x.f\;x)\;f\;x\\ &=(\lambda f\;x.f\;x)\\ &=1 \end{aligned}
\begin{aligned} (plus\;one\;two) &= (\lambda n\;m\;f\;x.n\;f\;(m\;f\;x))(\lambda f\;x.f\;x)(\lambda f\;xf\;(.f\;x))\\ &=(((\lambda f\;x.f\;x)\;f) (\lambda f\;x.f\;(f\;x)))\;f\;x\\ &=(\lambda f\;x.f\;(\lambda f\;x.f\;(f\;x)))\;f\;x\\ &=(\lambda f\;x.f\;(f\;(f\;x)))\;f\;x\\ &=(\lambda f\;x.f\;(f\;(f\;x)))\\ &=3 \end{aligned}

抽象乘法

mult = \m n f -> m (n f)

image.png

公式

\begin{aligned} (mult\;one\;two) &= (\lambda m\;n\;f.m\;(n\;f))(\lambda f\;x.f\;x)(\lambda f\;x.f\;(f\;x))\\ &=(\lambda f\;x.f\;x)(\lambda f\;x.f\;(f\;x))\\ &=(\lambda f\;x.f\;(f\;x))\\ &=2\\ (mult\;two\;two) &= (\lambda m\;n\;f.m\;(n\;f))(\lambda f\;x.f\;(f\;x))(\lambda f\;x.f\;(f\;x))\\ &=(\lambda f\;x.f\;(f\;x))(\lambda f\;x.f\;(f\;x))\\ &=(\lambda f\;x.(\lambda f\;x.f\;(f\;x))\;((\lambda f\;x.f\;(f\;x))\;x))\\ &=(\lambda f\;x.f\;(f\;(f\;\;(f\;x))))\\ &=4 \end{aligned}

所有的写所有的操作都会被规约进行优化，就像做数学题一样进行解题公式，因为λ演算就是从数学逻辑中发展出来的，所有的东西都通过λ表达式进行抽象，规约优化。

可以从这些中看出λ演算的图灵完备性，能做到任意图灵完备的语言做到的任何事

什么？你问我怎么循环？那当然是递归啦

随笔二 结语

如今的函数式语言都是脱胎于λ演算，更贴合编程语言的定义，而不是基于硬件的抽象。比如Lisp, scheme, Haskell， ML等语言。

现在的现代多范式语言也多少添加λ演算的特性，提高开发效率的同时也能更好的抽象业务，λ的抽象也不只是我在上面说的那些，还有很多抽象，比如谓词、命名常量、递归和不动点、组合子还有和η转换很像的消除抽象等等，由于λ演算过于学术，可能很多资料只能在论文中才能看到，比如说实数，复数虚数的抽象等等等等等等。。。。

但是碍于篇幅原因各位鱼油可以自行去查阅相关资料😋

最后你可能会在想为啥我在用其他语言的lambda表达式举例的时候，为什么没有列出java的。

那是因为java的“lambda表达式”并不是λ演算中的lambda表达式，我个人甚至觉得都不能叫做“lambda表达式”，它本质上只是一个匿名类的构造函数，为了代替new xxxx() {}实例化匿名类的语法糖。它需要依赖外部接口来确定自己的类型信息，jvm才能用其匹配相应的方法。匿名类也只是在创建非全局的类，它的匿名性是体现在它的作用域，是当前类的局部类。而lambda的匿名是表示这个函数并没有名字，不需要绑定任何变量就可以直接应用，这俩有本质的区别。正因为这样它的应用甚至需要依赖外部接口，比如无法做到((int x, int y) -> x + y)(1, 1)这样的直接应用。我不喜欢java社区的原因就是社区的人喜欢乱用名词以及自己造词，java的“lambda表达式”与其说是lambda表达式，不如说是实例化匿名类的方法之一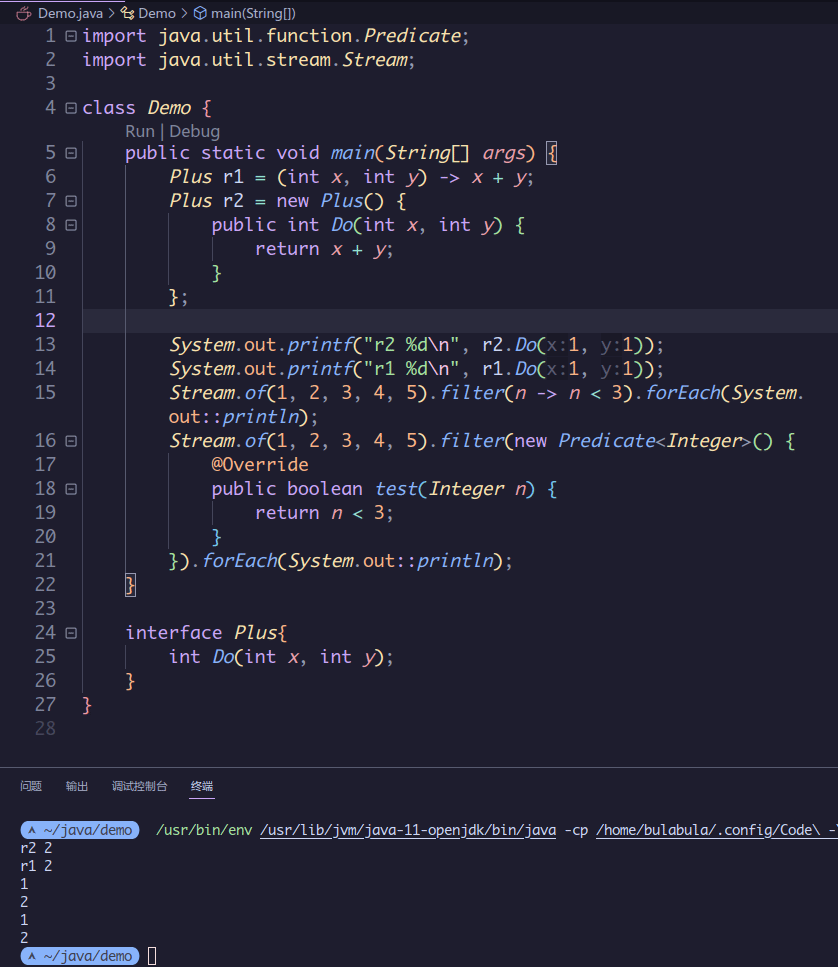image.png

   
10 点赞
0 关注
1 收藏


10 感谢 


23 回帖 
1.5K