文章来自公众号 技术乱舞

原文链接 ：https://mp.weixin.qq.com/s/M0mGAwuYK5lRLZN8Eve5xA

正则表达式匹配

刷题目前遇到动态规划题目中最难的一题，今天就与大家分享一下具体解题过程，在菜的路上越来约菜。

如果追忆会荡起涟漪，那么今天的秋红落叶和晴空万里都归你
https://aeneag.xyz

关注「技术乱舞」，一起进步！

LeetCode第十题，正则表达式匹配，是目前做过动态规划题目中最难的一题，个人认为也是这100题中最难的一题，也是结束100热题的最后一道。

题目描述

给你一个字符串 s 和一个字符规律 p，请你来实现一个支持 '.'和 '*'** **的正则表达式匹配。

• '.'** **匹配任意单个字符
• '*'** **匹配零个或多个前面的那一个元素

所谓匹配，是要涵盖 整个字符串 s 的，而不是部分字符串。

示例1：

输入 ：s = "aa" p = "a"

输出 ：false

解释 ："a" 无法匹配 "aa" 整个字符串。

示例2：

输入 ：s = "aa" p = "a*"*

输出 ：true

解释 ：因为 '*'** 代表可以匹配零个或多个前面的那一个元素, 在这里前面的元素就是 'a' 。因此，字符串 "aa" 可被视为 'a' **重复了一次。

示例3：

输入 ：s = "mississippi" p = "misis p*."

输出 ：false

提示：

• 1 <= s.length <= 20
• 1 <= p.length <= 30
• s 可能为空，且只包含从 a-z 的小写字母。
• p 可能为空，且只包含从 a-z 的小写字母，以及字符 . 和 *。
• 保证每次出现字符 * 时，前面都匹配到有效的字符

题目分析

执行过程

看到题目首先会想到用动态规划解题，dp数组到底表示什么呢？

首先建立S和P的二维数组：

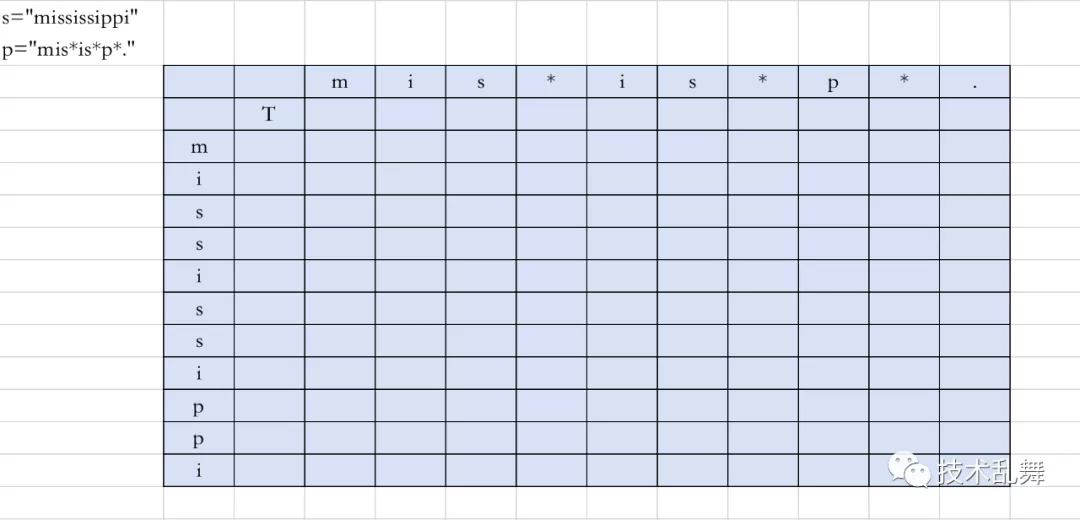
首先开始建立一个二维数组，最开始的样子，图上第一个True是行列都为空的时候，此时字符匹配，所以第一个是True。

那么接下来对这个二维数组初始化：

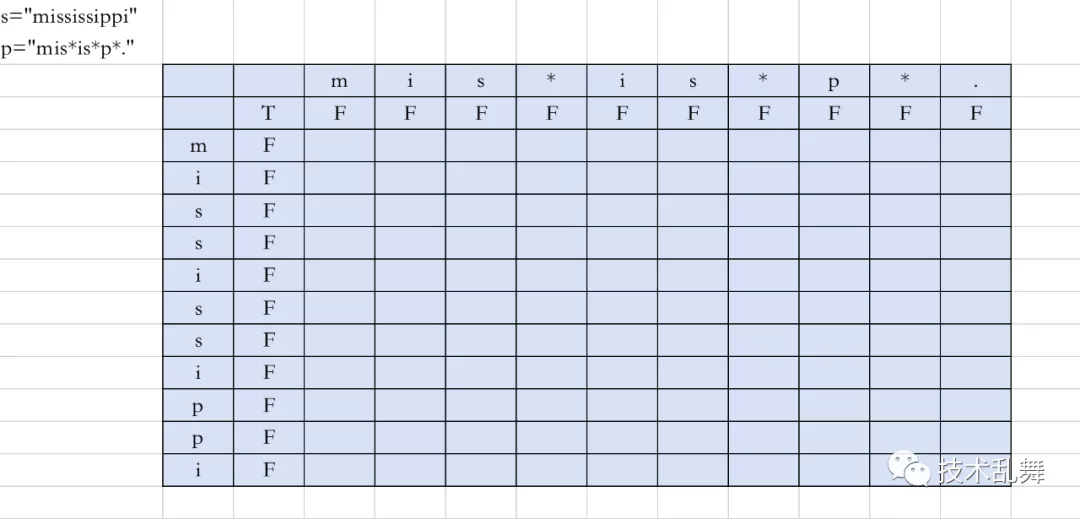
第一列所有的字符都与空字符无法匹配，所以全部填入False。

第一行的数据，与空字符无法匹配，填入False，当然此时一定要注意，如果当前列是 *** **号，那么就要看当前列的前二列是什么，如果是True，那么当前列也是True。用代码表示就是 dp[i][j] = dp[i][j-2]。

初始化完成后，就可以开始填表了：

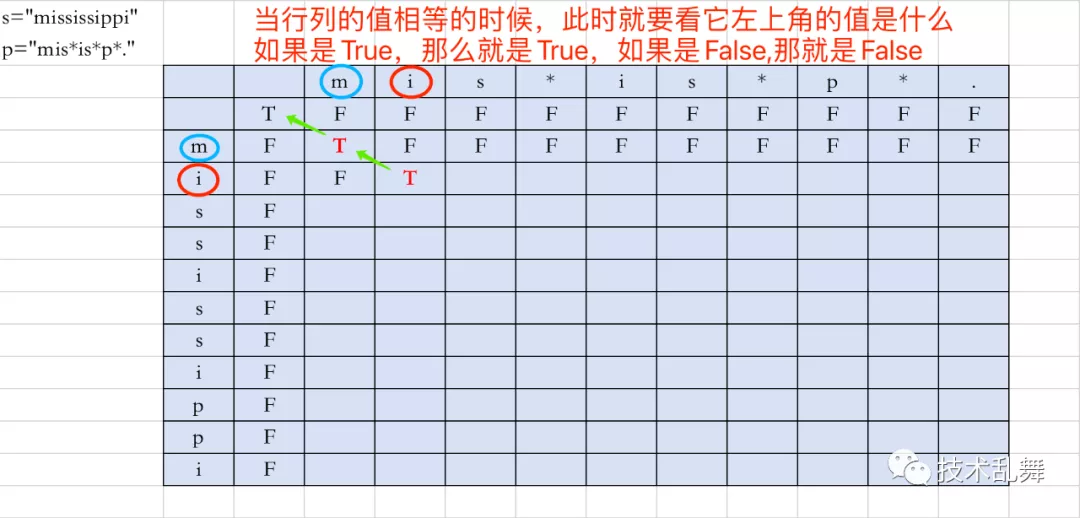
填表规则：

• 如果没有遇到*****和.** ** 只要行列字符不相同就填入False
• 如果遇到行列相同的情况，那么就看它左上方的状态是什么，如上图，是True就填True，代码表示dp[i][j] = dp[i-1][j-1]

为什么这么填呢，行列同时加入一个字符，并且两个字符相同，那如果看是否匹配那就看没加入之前是什么状态，用数组表示，就是查看左上方的状态。

接下来处理遇到 *** **号时：

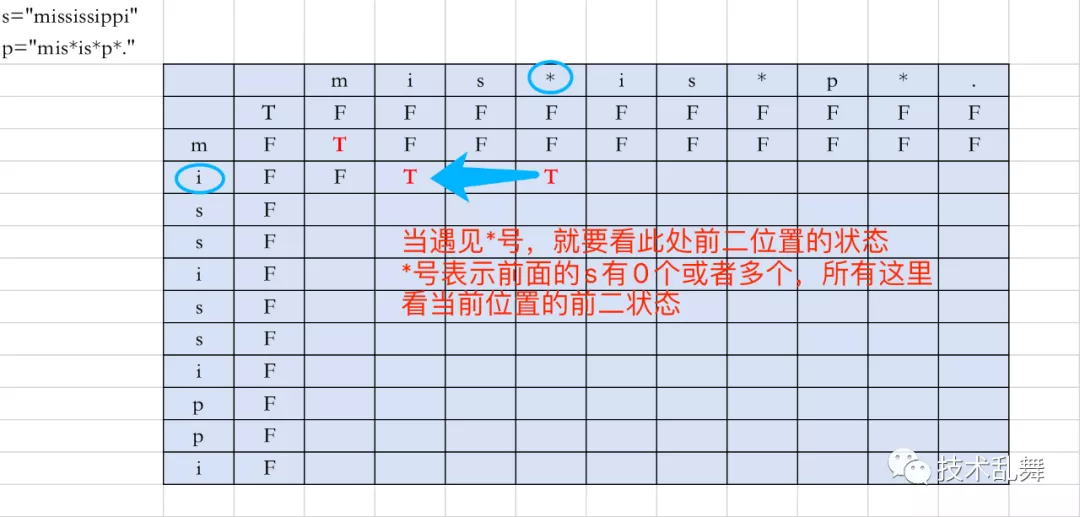
• 如上图所示，如果遇到***号，就看当前行前二位置的状态，代码表示 dp[i][j] = dp[i][j-2] **，如果是True，那么这里也是True，如果不是，下文讲解。

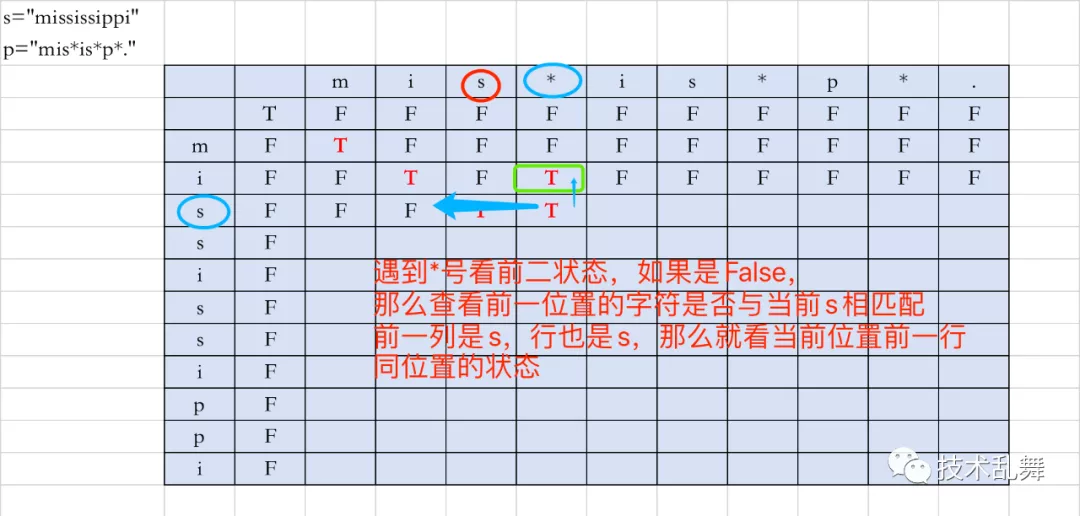
• 上图就是遇到了*号，当前行前二位置不匹配的情况，那么现在就查看 p[i-1] == s[i]，也就是图上*** **之前字符与当前行的字符是否相同，图中相同，那么当前状态就是dp[i][j] = dp[i-1][j]，就是复制上一行，当前位置的状态 ，只要不满足当前情况都是False。为什么复制上一行相同位置的状态，因为如果之前是True，那么这个时候又多一个相同的符号也可以，如果不是True，加上一个，同样也不匹配。

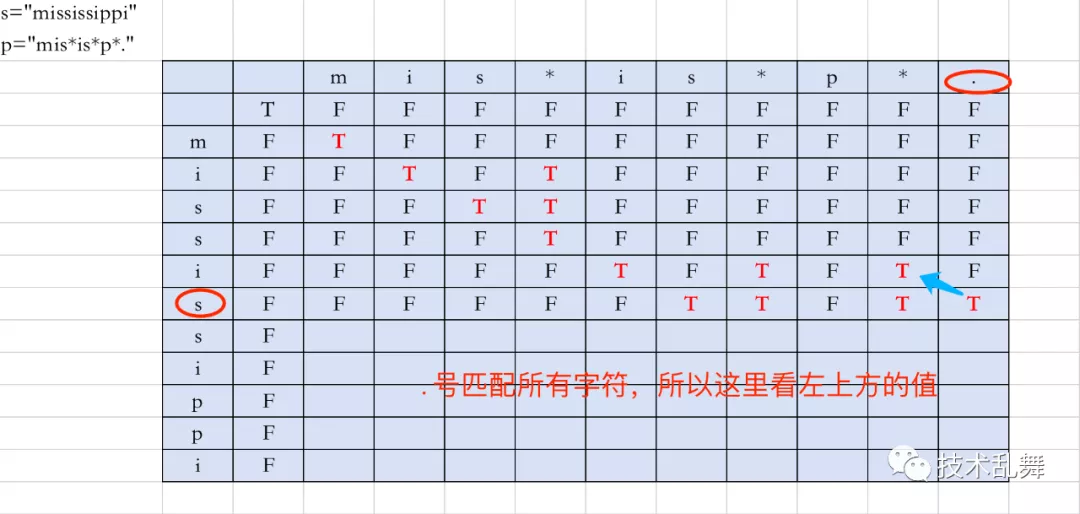
• 最后就是.** **号情况，这个遇到任何符号，都是代表匹配的意思，所以如上图所示，复制左上方状态即可。

遵循上文规则，即可在图表的最下方获得结果

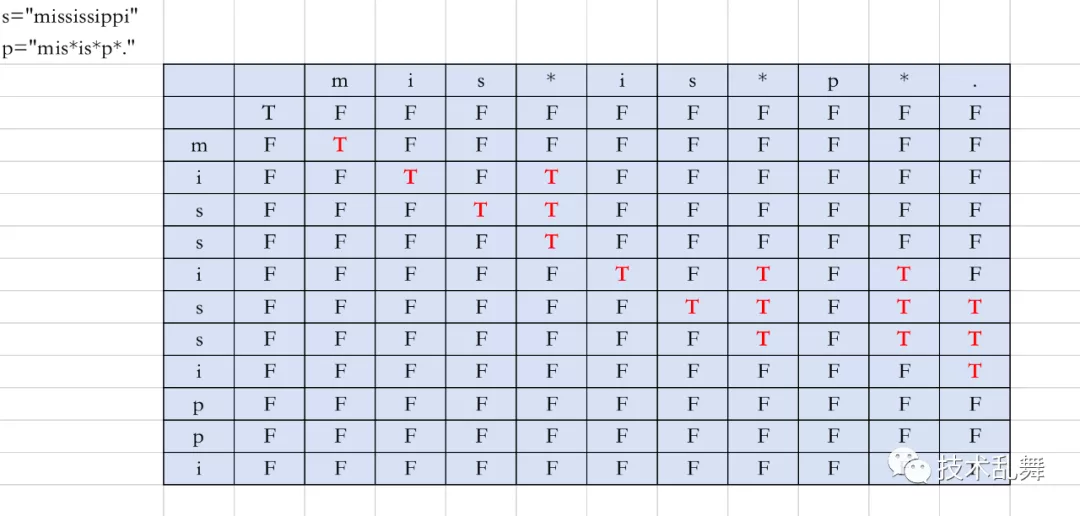
那么看一组准确的求解过程

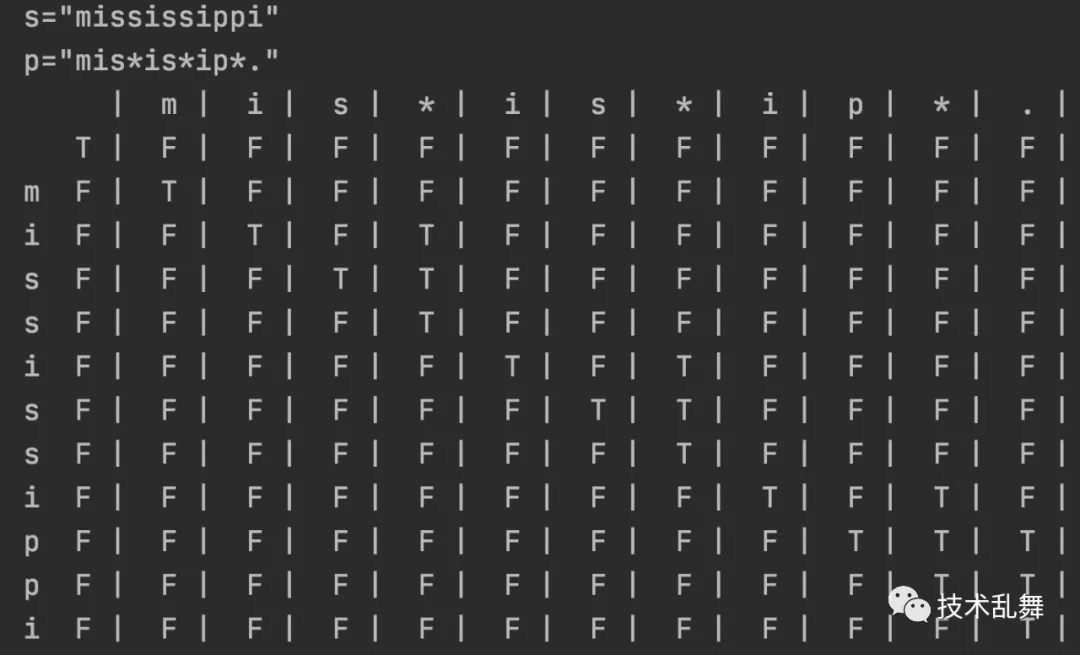
小结

dp状态数组更新过程：

1. 初始化数组全部为False，如果是*** **号，dp[i][j] = dp[i][j-2]。
2. 行列是相同字符或者遇到.号，状态与左上角相同，dp[i][j] = dp[i-1][j-1]
3. 遇到*号，两种情况

• 如果前二位置True，那么也是True，dp[i][j] = dp[i][j-2]
• 上面的情况不是True，那么，查看p[i-1] == s[i]** **是否相等，如果相等，此刻的状态与上一行当前位置状态相同，dp[i][j] = dp[i-1][j]

上面的过程也就是代码要实现的过程。

题解代码

代码中已详加注释，把分析过程实现即可。

class Solution {
public:
    //写代码时，犯了一个错误，就是用for循环获取s和p中的某个字符，导致初始化和计算过程出错
    bool isMatch(string s, string p) {
        //新建一个二维数组，并初始化，全部为False，注意要比s和p大一个
        vector<vector<bool>> dp(s.size()+1,vector<bool>(p.size()+1,false));
        //第一个状态设置为True
        dp[0][0] = true;
        //for循环初始化dp数组，遵循之前分析的过程
        for(int i = 1 ; i < dp[0].size() ; ++i){
            // for(auto &c : p){ //出错的地方，之前用for循环，脑袋卡壳了
            //获取当前行的第i个值
            char c = p[i-1];
            //查看是否匹配
            if(c == '*' )
                dp[0][i] = dp[0][i-2];
            //  }
        }
        //双for循环，填写二位数组状态值
        for(int i = 1 ; i < dp.size() ; ++i){
            //获取当前列的第i个值
            char c = s[i-1];
            for(int j = 1 ; j < dp[i].size() ; ++j){
                //获取当前行的第j个值
                char m = p[j-1];
                //比较字符
                if(c == m || m == '.'){
                    dp[i][j] = dp[i-1][j-1];
                }else if(m == '*'){//如果是*号，接下来要干什么
                    //这里if防止数组越界 j > 1
                    if(j > 1){
                        //if 判断语句，如图分析一般用代码实现
                        if(dp[i][j-2] == true)//前二位置是true，那么这里也是true
                            dp[i][j] = true;
                        else{
                            //获取前一个位置的字符
                            char m_prv = p[j-2];
                            //判断是否相同，如果相同，就与上一行当前位置状态一样
                            if(m_prv == c || m_prv == '.')
                                dp[i][j] = dp[i-1][j];
                        }
                    }
                }
            }
        }
        return dp[s.size()][p.size()];
    }
};

代码可以在LeetCode上完美运行，如果想要推理它的状态填表过程，提供线下代码。

#include <iostream>
#include <vector>
using namespace std;
//写代码时，犯了一个错误，就是用for循环获取s和p中的某个字符，导致初始化和计算过程出错
bool isMatch(string s, string p) {
    //新建一个二维数组，并初始化，全部为False，注意要比s和p大一个
    vector<vector<bool>> dp(s.size()+1,vector<bool>(p.size()+1,false));
    //第一个状态设置为True
    dp[0][0] = true;
    //for循环初始化dp数组，遵循之前分析的过程
    for(int i = 1 ; i < dp[0].size() ; ++i){
        // for(auto &c : p){ //出错的地方，之前用for循环，脑袋卡壳了
        //获取当前行的第i个值
        char c = p[i-1];
        //查看是否匹配
        if(c == '*' && i > 1)
            dp[0][i] = dp[0][i-2];
        if(i == 1 && c == '*')
            dp[0][i] = true;
        //  }
    }
    //双for循环，填写二位数组状态值
    for(int i = 1 ; i < dp.size() ; ++i){
        //获取当前列的第i个值
        char c = s[i-1];
        for(int j = 1 ; j < dp[i].size() ; ++j){
            //获取当前行的第j个值
            char m = p[j-1];
            //比较字符
            if(c == m || m == '.'){
                dp[i][j] = dp[i-1][j-1];
            }else if(m == '*'){//如果是*号，接下来要干什么
                //这里if防止数组越界 j > 1
                if(j > 1){
                    //if 判断语句，如图分析一般用代码实现
                    if(dp[i][j-2] == true)//前二位置是true，那么这里也是true
                        dp[i][j] = true;
                    else{
                        //获取前一个位置的字符
                        char m_prv = p[j-2];
                        //判断是否相同，如果相同，就与上一行当前位置状态一样
                        if(m_prv == c || m_prv == '.')
                            dp[i][j] = dp[i-1][j];
                    }
                }
            }
        }
    }
    printf("     |");
    for(int i = 0 ; i < p.size();++i)
        printf("  %c |",p[i]);
    printf("\n");
    for(int i = 0 ; i < dp.size() ; ++i){
        if(i > 0)
            printf("%c",s[i-1]);
        for(int j = 0 ; j < dp[0].size();++j){
            if(dp[i][j])
                if(i == 0)
                    printf("   T |");
                else
                    printf("  T |");
            else
                printf("  F |");
        }
        printf("\n");
    }
    return dp[s.size()][p.size()];
}
int main(void) {
    std::cout << "Hello, World!" << std::endl;
    string s="mississippi";
    string p="mis*is*ip*.";
    printf("s=\"mississippi\"\n");
    printf("p=\"mis*is*ip*.\"\n");
    isMatch(s,p);
    return 0;
}

总结

动态规划最难的就是如何想出状态方程，算法博大精深，值得一直学习。今天的分享就到这了，如果你喜欢我的文章，欢迎关注，可以点点下方在看，随缘分享技术文与生活文。

欢迎关注 #公众号：技术乱舞 一起交流

灵魂碰撞