本文将介绍一种用于分类问题的后处理技巧（Trick），出自EMNLP 2021 Findings的一篇论文《When in Doubt: Improving Classification Performance with Alternating Normalization》。经过实测，CAN（Classification with Alternating Normalization）确实多数情况下能提升多分类问题的效果（CV、NLP通用），而且几乎没有增加预测成本，因为它仅仅只是对预测结果的重新归一化操作

CAN的思想

有趣的是，其实CAN的思想非常朴素，朴素到我们每个人几乎都用过。具体来说，假设考试中有10道选择题，前9道你都比较有信心，第10题完全不会只能瞎蒙，但是你发现前面9题选A、B、C、D的比例是3:3:2:2，那么第10题在蒙的时候，你会不会更倾向于C和D？如果是更极端的情况，你发现前面9题选A、B、C的都有，但就是没有选D的，那你蒙第10题的时候，会不会更倾向于D？

回到分类任务上，假设现在有一个二分类问题，模型对于输入a给出的预测结果是p^{(a)}=[0.05, 0.95]，那么我们就可以给出预测类别为1；接下来，对于输入b，模型给出的预测结果是p^{(b)}=[0.5,0.5]，这种结果是最不确定的，我们也不知道应该输出哪个类别

但是，假如我告诉你：

1. 类别必然是0或1其中之一
2. 两个类别出现的概率各为0.5

在已知这两点「先验」信息的情况下，由于前一个样本的预测结果为1，那么基于朴素的均匀思想，我们是否会更倾向于将后一个样本预测为0，以得到一个满足第二点「先验」的预测结果？

这些简单的例子背后，有着跟CAN同样的思想，其实就是用「先验分布」来校正「低置信度」的预测结果，使得新的预测结果的分布更接近先验分布

Top-k熵

准确地说，CAN是针对低置信度预测结果的后处理手段，所以我们首先要有一个衡量预测结果不确定性的指标。常见的度量是「熵」，对于p=[p_1,p_2,...,p_m]，定义为

虽然熵是一个常见的选择，但其实它得出的结果并不总是符合我们的直观理解。例如对于p^{(a)}=[0.5, 0.25,0.25]和p^{(b)}=[0.5,0.5,0]，直接套用公式得到H(p^{(a)})>H(p^{(b)})，但如果让人主观去评价这两个概率分布，显然我们会认为p^{(b)}比p^{(a)}更不确定，所以直接用熵还不够合理

客观地讲，熵值越大，表示这个系统内部越不稳定。如果要与置信度联系起来，熵值越大，置信度越低

一个简单的修正是只用前top-k个概率值来算熵，假设p_1,p_2,...,p_k是概率最高的k个值，那么

其中，\mathcal{T}是一个取向量最大的前k个值的操作\mathbb{R}^{m}\to \mathbb{R}^{k}。我们可以将式(2)带入式(1)展开得

其中，\tilde{p}_i = p_i / \sum\limits_{i=1}^k p_i

交替归一化（Alternating Normalization）

这一部分我先给出论文中的算法步骤描述，下一节我会手动模拟一遍计算过程

Step1

设列向量\mathbf{b}_0\in \mathbb{R}^m为输入样本x对应各类别的概率分布，m表示类别数。我们生成一个n\times m的概率矩阵A_0，A_0其实是n个置信度非常高的样本对各个类别的预测概率向量拼接而得，通过将A_0和\mathbf{b}_0进行拼接得到一个(n+1)\times m的矩阵L_0

Step2

第二步是一个迭代的过程，具体来说，首先对矩阵L_0进行列归一化（使得每列求和为1），然后进行行归一化（使得每行求和为1）。进行算法步骤前，先定义一个向量对角化操作：

\mathcal{D}(\mathbf{v})会将列向量\mathbf{v}\in \mathbb{R}^n转换为n\times n的对角矩阵，对角线元素即原本的向量元素

列归一化

其中，参数\alpha \in \mathbb{N}^+控制着\mathbf{b}_0收敛到高置信度的速度（越大速度越快，默认取1）；\mathbf{e}\in \mathbb{R}^{n+1}是全1的列向量。经过式(4)的变换后，矩阵S_d\in \mathbb{R}^{(n+1)\times m}是L_{d-1}矩阵的列归一化形式；\Lambda_S^{-1}是\Lambda_S的逆矩阵

行归一化

其中，\mathbf{e}\in \mathbb{R}^{m}仍然是全1的列向量，只不过此时它的维度是m维的；矩阵L_d\in \mathbb{R}^{(n+1)\times m}是行归一化的（但L_d并不是具体某个矩阵的行归一化形式）；\Lambda_q \in \mathbb{R}^{m\times m}是一个对角矩阵，对角线上的元素是各类别的分布占比

例如

\Lambda_q = \begin{bmatrix}0.2&0&0\\0&0.4&0\\0&0&0.4\end{bmatrix}

表示这是一个三分类问题，并且各个类别的比例为1:2:2

Step3

Step2循环迭代d次后得到的矩阵L_d：

其中，\mathbf{b}_d就是根据「先验分布」调整后的新的概率分布

注意，这个过程需要我们遍历每个低置信度的预测结果，也就是说逐个样本进行修正，而不是一次性修正的。并且虽然迭代过程中A_0里对应的各个样本的预测概率也都随之更新了，但那只是临时结果，最后都是弃之不用的，每次修正都是用原始的A_0

模拟计算AN（Alternating Normalization）

首先我们设置一些矩阵和参数

稍微解释一下，A_0根据原算法描述是n个置信度比较高的样本的预测概率分布进行拼接，可以看出只有3个样本置信度比较高，并且他们的预测类别分别为2，0，2；b_0是某样本x的预测概率，因为是概率分布，所以必须满足求和为1；\Lambda_q是三个类别的样本比例，可以看出第一个类别的数据非常多

首先是列归一化

仔细观察矩阵S_d，它每列求和都是1，也就是列归一化，如果我们追根溯源的话，实际上S_d就是L_0对每列求和，然后将L_0每列元素除以该和

接着是行归一化

我们只需要L_1的最后一行，即\mathbf{b}_1=\begin{bmatrix}23/25&0&2/25\end{bmatrix}^T，可以看，原本\mathbf{b}_0的概率分布是\begin{bmatrix}0.5 &0&0.5\end{bmatrix}^T，经过「先验」调整后的类别明显偏向数据占比比较多的第一类，并且\mathbf{b}_1向量求和为1，符合概率的定义

实际上这个过程用Python实现也非常简单，下面就是我自己写的一个代码，变量命名与公式中的变量名完全一致

import numpy as np

n, m, d, alpha = 3, 3, 5, 1
# n: 样本数量
# m: 类别数
# d: 迭代次数
# alpha: 次方

def softmax(arr):
    return np.exp(arr) / np.sum(np.exp(arr))

A_0 = np.array([[0.2, 0, 0.8], [0.9, 0.1, 0], [0, 0, 1]])
# A_0 = softmax(np.random.randn(n, m))

b_0 = np.array([0.5, 0, 0.5])
# b_0 = softmax(np.random.randn(m))

L_0 = np.vstack((A_0, b_0)) # (n+1) * m

Lambda_q = np.diag( np.array([0.8, 0.1, 0.1]) )
# Lambda_q = np.diag( softmax(np.random.randn(m)) )

print("预测概率：", b_0)
print("各类别样本数量分布：", np.diag(Lambda_q, 0))

L_d_1 = L_0
for _ in range(d):
    Lambda_S = np.diag( np.dot((L_d_1 ** alpha).T, np.ones((n + 1))) )
    S_d = np.dot((L_d_1 ** alpha), np.linalg.inv(Lambda_S))
    Lambda_L = np.diag( np.dot(np.dot(S_d, Lambda_q), np.ones((m))) )
    L_d_1 = np.dot( np.dot(np.linalg.inv(Lambda_L), S_d), Lambda_q )
    print("根据先验调整后的概率：", L_d_1[-1:])

参考实现

下面给出苏剑林大佬的实现，他的代码中将Top-k熵做了个归一化，保证H_{\text{top-k}}(p)\in [0,1]，这样比较好确定阈值（即代码中的threshold）

import numpy as np

# 预测结果，计算修正前准确率
y_pred = np.array([[0.2, 0.5, 0.2, 0.1],
          [0.3, 0.1, 0.5, 0.1],
          [0.4, 0.1, 0.1, 0.4],
          [0.1, 0.1, 0.1, 0.8],
          [0.3, 0.2, 0.2, 0.3],
          [0.2, 0.2, 0.2, 0.4]])
num_classes = y_pred.shape[1]
y_true = np.array([0, 1, 2, 3, 1, 2])
acc_original = np.mean([y_pred.argmax(1) == y_true])
print('original acc: %s' % acc_original)

# 从训练集统计先验分布
# prior = np.zeros(num_classes)
# for d in train_data:
#     prior[d[1]] += 1.
# prior /= prior.sum()
prior = np.array([0.2, 0.2, 0.25, 0.35])


# 评价每个预测结果的不确定性
k = 3
y_pred_topk = np.sort(y_pred, axis=1)[:, -k:]
y_pred_topk /= y_pred_topk.sum(axis=1, keepdims=True) # 归一化
y_pred_entropy = -(y_pred_topk * np.log(y_pred_topk)).sum(1) / np.log(k) # top-k熵
print(y_pred_entropy)

# 选择阈值，划分高、低置信度两部分
threshold = 0.9
y_pred_confident = y_pred[y_pred_entropy < threshold] # top-k熵低于阈值的是高置信度样本
y_pred_unconfident = y_pred[y_pred_entropy >= threshold] # top-k熵高于阈值的是低置信度样本
y_true_confident = y_true[y_pred_entropy < threshold]
y_true_unconfident = y_true[y_pred_entropy >= threshold]

# 显示两部分各自的准确率
# 一般而言，高置信度集准确率会远高于低置信度的
acc_confident = (y_pred_confident.argmax(1) == y_true_confident).mean()
acc_unconfident = (y_pred_unconfident.argmax(1) == y_true_unconfident).mean()
print('confident acc: %s' % acc_confident)
print('unconfident acc: %s' % acc_unconfident)

# 逐个修改低置信度样本，并重新评价准确率
right, alpha, iters = 0, 1, 1 # 正确的个数，alpha次方，iters迭代次数
for i, y in enumerate(y_pred_unconfident):
    Y = np.concatenate([y_pred_confident, y[None]], axis=0) # Y is L_0
    for _ in range(iters):
        Y = Y ** alpha
        Y /= Y.sum(axis=0, keepdims=True)
        Y *= prior[None]
        Y /= Y.sum(axis=1, keepdims=True)
    y = Y[-1]
    if y.argmax() == y_true_unconfident[i]:
        right += 1

# 输出修正后的准确率
acc_final = (acc_confident * len(y_pred_confident) + right) / len(y_pred)
print('new unconfident acc: %s' % (right / (i + 1.)))
print('final acc: %s' % acc_final)

实验结果

那么，这样简单的后处理，究竟能带来多大的提升呢？原论文给出的实验结果是相当可观的：

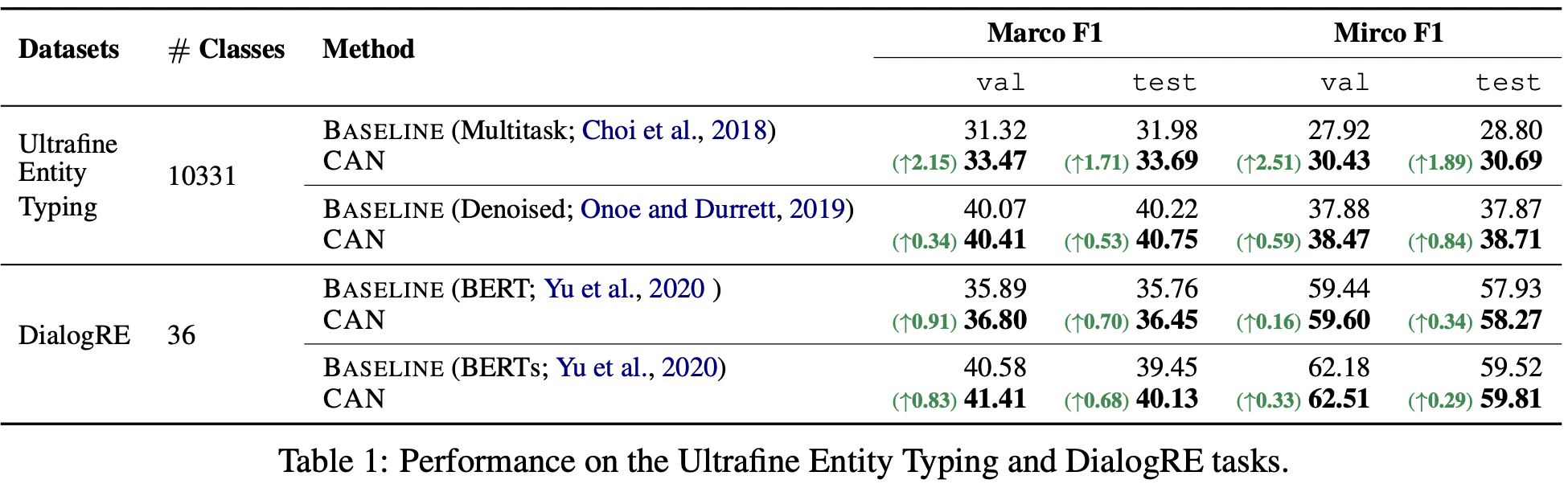
大体来说，类别数越多，效果提升越明显，如果类别数比较少，那么提升可能比较微弱甚至会下降

One More Thing

一个很自然的疑问是为什么不直接将所有低置信度的结果跟高置信度的结果拼在一起进行修正，而是要逐个修正？其实很好理解，CAN本意是要借助「先验分布」，结合高置信度结果来修正低置信度，在这个过程中如果掺入的低置信度结果越多，最终的偏差可能就越大，因此理论上逐个修正会比批量修正更为可靠

References

• When in Doubt: Improving Classification Performance with Alternating Normalization
• CAN：借助先验分布提升分类性能的简单后处理技巧