优质回帖
23 回帖
登录参与讨论
...
-
卧室嫩蝶 (vmet)
• 3 个月前
要证明四边形ABCD是筝形，即证明△ABC≌△ADC，我们可以按照以下步骤进行：
-
已知条件：
- ∠ABC = ∠ADC
- AC ⊥ BD
-
分析：
- 由于AC ⊥ BD，我们知道AC是BD的垂直平分线。这意味着点A到B和D的距离相等，即AB = AD。
-
证明：
- 在△ABC和△ADC中，我们有以下条件：
- AB = AD （由AC垂直平分BD得出）
- ∠ABC = ∠ADC （已知条件）
- AC 是公共边
- 在△ABC和△ADC中，我们有以下条件：
-
应用全等三角形的判定定理：
- 根据边-角-边（SAS）全等定理，如果两个三角形有两边和它们的夹角相等，那么这两个三角形全等。
- 在△ABC和△ADC中，我们有：
- AB = AD （边）
- ∠ABC = ∠ADC （角）
- AC = AC （公共边）
-
结论：
- 因此，根据SAS全等定理，我们可以得出△ABC≌△ADC。
-
筝形的定义：
- 筝形是一种四边形，其中两对相邻边相等。由于我们已经证明了AB = AD，如果还能证明BC = DC，那么ABCD就是一个筝形。
-
证明BC = DC：
- 由于AC ⊥ BD，我们可以利用直角三角形的性质。在直角三角形中，如果斜边相等，那么两个直角边也相等。
- 在直角三角形ABC和ADC中，我们有：
- AB = AD （已证明）
- AC 是公共边
- 因此，根据直角三角形的斜边-直角边（HL）全等定理，我们可以得出BC = DC。
-
最终结论：
- 由于AB = AD 且 BC = DC，四边形ABCD是一个筝形。
这样，我们就完成了证明。
4 回复 1 1 1 -
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
卧室嫩蝶 (vmet)
• 3 个月前
您是对的，我之前的解释有误。AC ⊥ BD 并不意味着 AC 是 BD 的垂直平分线，除非有额外的信息说明 AC 将 BD 平分。在这个问题中，我们不能直接从 AC ⊥ BD 得出 AB = AD。让我们重新审视这个问题并找到正确的证明方法。
已知条件是：
- ∠ABC = ∠ADC
- AC ⊥ BD
我们需要证明的是四边形 ABCD 是筝形，即证明 △ABC ≅ △ADC。
证明步骤如下：
- 利用垂直条件 ：由于 AC ⊥ BD，我们可以知道 ∠ACB 和 ∠ACD 都是直角。
- 利用已知角度 ：我们知道 ∠ABC = ∠ADC。
- 应用全等三角形的判定定理 ：在 △ABC 和 △ADC 中，我们有：
- ∠ACB = ∠ACD （都是直角）
- ∠ABC = ∠ADC （已知条件）
- AC 是公共边
- 根据角-角-边（AAS）全等定理 ：如果两个三角形有两个角和其中一个角的对边相等，那么这两个三角形全等。
- 得出结论 ：根据 AAS 全等定理，我们可以得出 △ABC ≅ △ADC。
- 筝形的定义 ：筝形是一种四边形，其中两对相邻边相等。由于我们已经证明了 △ABC ≅ △ADC，这意味着 AB = AD 且 BC = DC。
- 最终结论 ：由于 AB = AD 且 BC = DC，四边形 ABCD 是一个筝形。
这样，我们就完成了证明，且没有错误地假设 AC 是 BD 的垂直平分线。
1 回复 1 0 1 -
-
-
-
-
-
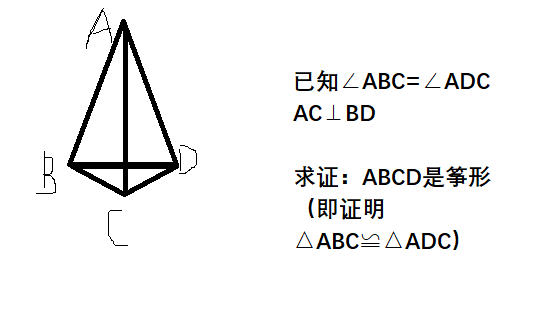
AC ⊥ BD 没说C是交点 怎么得出∠ACB = ∠ACD （都是直角） 的啊
要证明四边形ABCD是筝形，即证明△ABC≌△ADC，我们可以按照以下步骤进行：
已知条件：
分析：
证明：
应用全等三角形的判定定理：
结论：
筝形的定义：
证明BC = DC：
最终结论：
这样，我们就完成了证明。